Outline
- 강화학습 개요
- 강화학습 기초
- 다이나믹 프로그래밍(Dynamic Programming)
- 큐러닝 (Q-Learning)
1. 강화학습의 개요
[1/2] 강화학습이란?
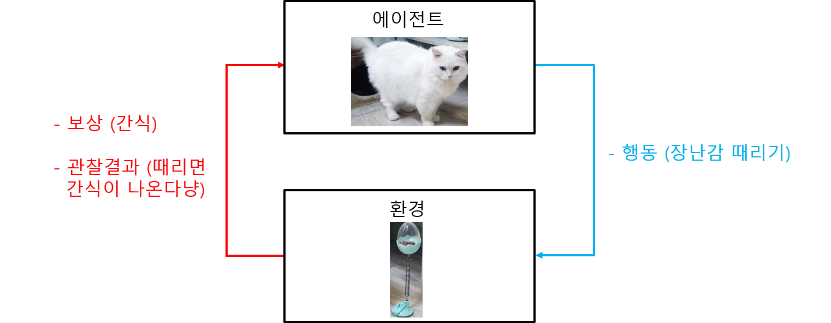 그림 1: Schematic depiction of Reinforcement Learning (RL)
그림 1: Schematic depiction of Reinforcement Learning (RL)
- 에이전트(Agent)가 환경(Environment)으로 부터 얻어지는 보상정보(Reward)를 통해 좋은 행동을 점점 더 많이 하도록 하는 학습 방법
[2/2] 강화학습의 장점
- 기존의 방식으로 풀기 어려웠던 복잡한 문제들을 해결할 수 있음
- 학습 데이터가 없어도 경험으로부터 학습할 수 있음
- 인간의 학습방법과 굉장히 유사하다. 따라서 학습이 직관적이고 완벽함을 추구하며 현실세계의 문제들을 해결할 수 있음
2. 강화학습의 기초
[1/6] Markov Decision Process (MDP)
- MDP란 강화학습 같은 순차적으로 행동을 결정하는 문제를 정의할 때 사용하는 방법
- MDP의 구성요소는 크게 다섯가지임. 상태(state), 행동(action), 보상함수(reward), 상태변환확률(state transition probability), 감가율(discount factor)
- 모든 강화학습은 MDP를 “사용자”가 정의하는 것 부터 시작
[2/6] Value Function
-
반환값(Return): 에이전트가 실제로 환경을 탐험하며 받은 보상
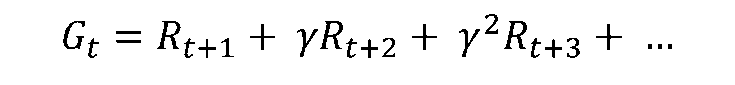
-
가치함수(Value Function): 에이전트가 어떠한 상태에 있을때 얼마의 보상을 받을 것인지에 대한 기댓값. 매 시행마다 값이 다르기 때문에 기댓값을 사용
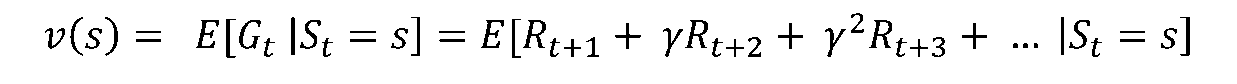
[3/6] Policy
- 어떤 상태에서 에이전트가 할 행동에 대한 확률
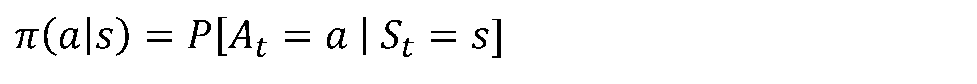
[4/6] Bellman Expectation Equation
- 벨만 기대 방정식이란 현재 상태의 가치함수와 다음상태의 가치함수 사이의 관계를 말해주는 방정식
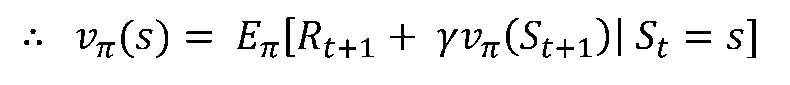
[5/6] Q-Function
- 큐함수(q-function)는 어떤 ‘상태’에서 어떤 ‘행동’이 얼마나 좋은지 알려주는 함수. 행동 가치함수라고도 함
- 큐함수는 상태와 행동이라는 두가지 변수를 가짐
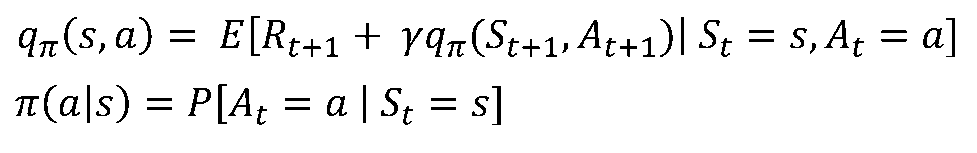
[6/6] Bellman Optimality Equation
- 가치함수는 정책을 정하고 더 좋은 정책을 찾아내는 것에 대한 지표역할을 함
- 최적의 가치함수는 다음과 같이 구할 수 있음
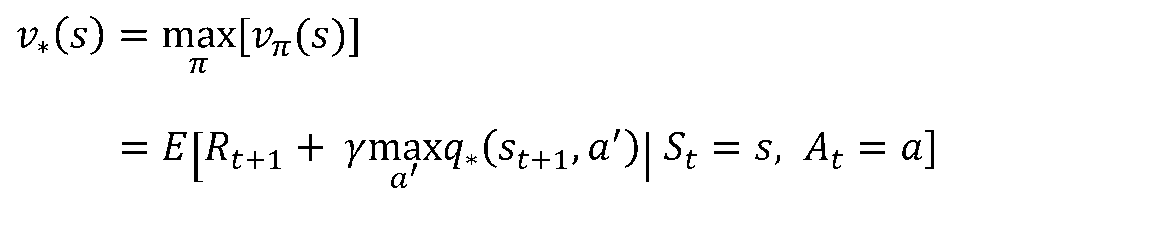
3. 다이나믹 프로그래밍 (Dynamic Programming)
[1/8] 동적 프로그래밍 이란?
- 동적 → 기억하기
- 프로그래밍 → (순차적 프로세스에 대한) 테이블 만들기
- 큰 문제를 한 번에 해결하기 힘들때 작은 여러개의 문제로 나누어서 푸는 기법
[2/8] 그렇다면 무엇을 어떻게 작은문제로 나누어서 풀까?
- 우리가 구하고 싶은것: 각 상태의 가치함수
- 모든 상태에 대해 가치함수를 구하고 iteration을 돌며가치함수를 업데이트 함
[3/8] 가치함수가 구해지는 과정 (벨만방정식 푸는 과정)
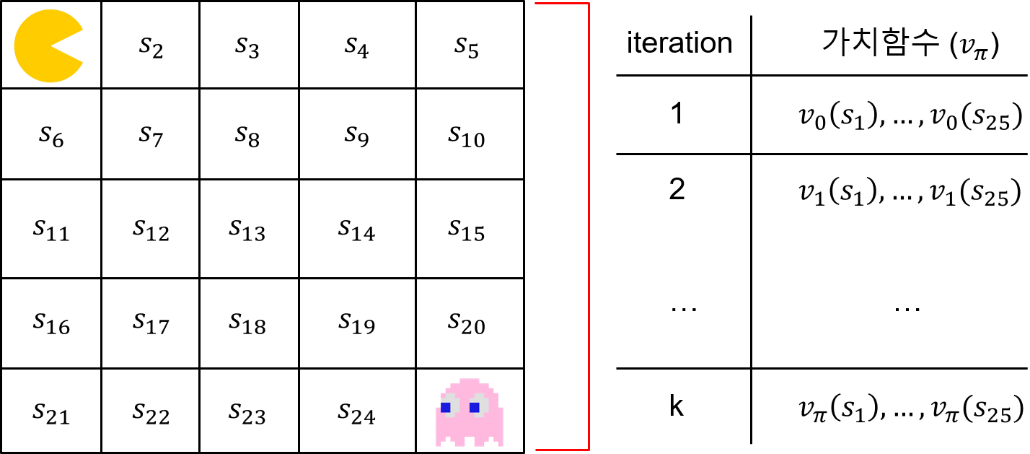 그림 2: The process of finding the value function (i.e. the process of solving the Bellman equation)
그림 2: The process of finding the value function (i.e. the process of solving the Bellman equation)
[4/8] 정책 이터레이션: 정책 평가와 정책 발전
- 핵심은 다이나믹 프로그래밍으로 벨만방정식을 풀어서 가치함수를 구하는 과정을 이해하는것!
- 이 과정을 정책 이터레이션이라고 함
- 처음에는 무작위 행동을 한 후 이터레이션을 돌며 가치함수를 최적화 시켜나감
- 최적화 과정은 정책 평가(Policy Evaluation)와 정책 발전(Policy Improvement)으로 나누어짐
[5/8] 정책 평가 (from 정책 이터레이션)
- 어떤 정책(Policy)이 있을때 그 정책을 정책 평가를 통해 얼마나 좋은지 판단하고 그 결과를 기준으로 더 좋은 정책으로 발전시킴
- 그렇다면 정책을 어떻게 평가할 수 있을까?
-
그 근거는 바로 다이나믹 프로그래밍으로 구한 각각의 상태에 대한 가치함수가 됨
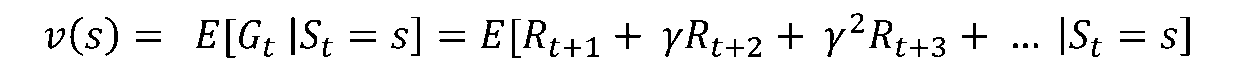
- 위 수식은 각각의 상태에 대한 아주 먼 미래까지 고려해야하기 때문에 계산량이 급격하게 늘어남
- 하지만 다이나믹 프로그래밍으로 이터레이션을 돌며 가치함수를 최적화 할 수 있음!
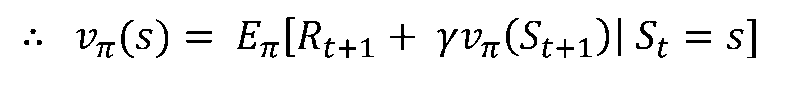
- 정책평가 과정
-
현재 상태 𝑠 에서 갈 수있는 다음 상태 𝑠′ 에 대한 가치함수를 불러옴
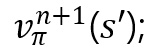
보라색 부분 중 하나 (그림 3) -
가치함수에 감가율을 곱하고 그 상태로 가는 것에 대한 보상을 더함
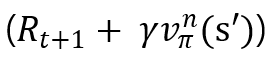
-
(2)에서 구한 값에 그 행동을 취할 확률(정책)을 곱하여 기댓값 형태로 나타냄
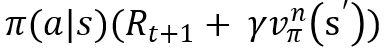
-
(3)을 모든 가능한 행동에 대해 반복하고 그 값을 더함
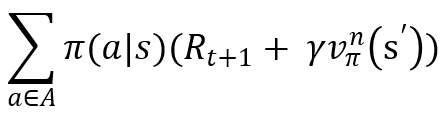
(5) 결과를 n+1 가치함수로 사용
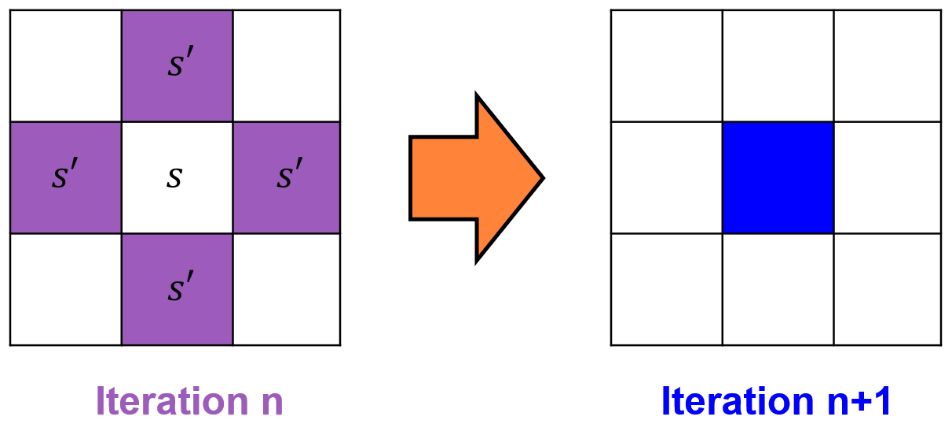 그림 3: Policy evaluation process using Dynamic programming algorithm in a grid world
그림 3: Policy evaluation process using Dynamic programming algorithm in a grid world
[6/8] 정책 발전 (from 정책 이터레이션)
- 정책 평가를 바탕으로 어떻게 정책을 발전시킬 수 있을까?
- 가치함수 최적화 전에는 무작위 행동을 하고 점점 가치함수가 높은 행동을 더 많이 하도록 학습함
- 가장 유명한 방법중 하나인 탐욕 정책 발전(Greedy Policy Improvement)를 사용함
-
정책에 대한 평가를 거치면 큐함수(Q-function)을 이용하여 행동에 대한 가치함수를 알 수 있음
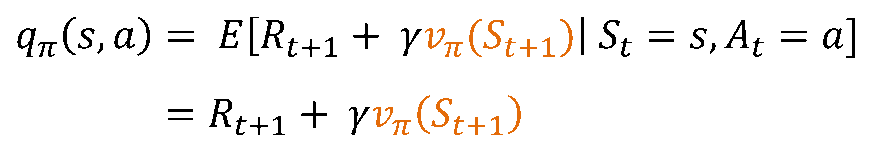
- 상태 𝑠에서 큐함수들을 비교하여 가장 큰 큐함수를 가지는 행동, 즉 행동 가치함수값이 가장 높은 행동을 선택함. 따라서 더 높은 보상을 주는 행동을 반복하도록 학습됨.
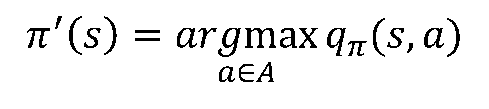
[7/8] 가치 이터레이션
- 가치 이터레이션(Value iteration)이란 현재의 가치함수가 최적은 아니지만 최적이라는 전제하에 각 상태에 대한 가치함수를 업데이트 하는 방법 (벨만최적방정식 사용)
- 벨만 기대방정식은 기댓값 형태이기 때문에 정책을 고려했었음. 하지만 벨만 최적방정식에서는 현재 상태에서 가능한 최고의 가치함수 값을 고려하면 됨
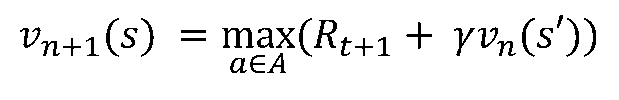
[8/8] 동적 프로그래밍의 한계
(1) 계산 복잡도 (i.e. 5x5 그리드 월드가 아니라 nxn이라면?)
(2) 차원의 저주 (i.e. 그리드 월드처럼 2차원이 아니라 n차원이라면?)
(3) 환경에 대한 완벽한 정보를 알아야 한다 (우리는 실제로 세상을 탑뷰로 바라보며 모든 환경에 대한 정보를 인지하고 있는가?)
4. Q-Learning
[1/6] 학습 방법
- 사람은 바둑을 어떻게 둘까? 다이나믹 프로그래밍때 처럼 한칸한칸 모든 경우의 수를 매 턴마다 생각하면서 둘까?
- 많은 경우가 일단 해보고 복기를 하고 복기 내용을 바탕으로 학습하여 더욱 잘해지는 과정을 반복한다.
- 강화학습은 사람의 학습방법처럼 겪은 경험으로 부터 가치함수를 업데이트 함
[2/6] 예측과 제어
- 에이전트는 환경과 상호작용을 통해 주어진 정책에 대한 가치함수를 학습할 수 있음
-
이를 예측(prediction)이라고 함 (앞에서 얘기했던 정책 평가에 해당) e.g.) 몬테카를로 예측, 시간차 예측
- 또한 가치함수를 토대로 정책을 끊임없이 발전시켜 나가 최적의 정책을 학습할 수 있음. 이를 제어(control)라고 함 (앞에서 얘기했던 정책 발전에 해당) e.g.) SARSA
[3/6] 몬테카를로 예측 (Monte Carlo Prediction)
- 가치함수에 대한 모델을 모르는 경우에도 몬테카를로 예측을 통해 가치함수를 추정하는 것이 가능함
-
가치함수를 추정할때 에이전트가 환경과 상호작용한 한 에피소드를 여러번 샘플링함
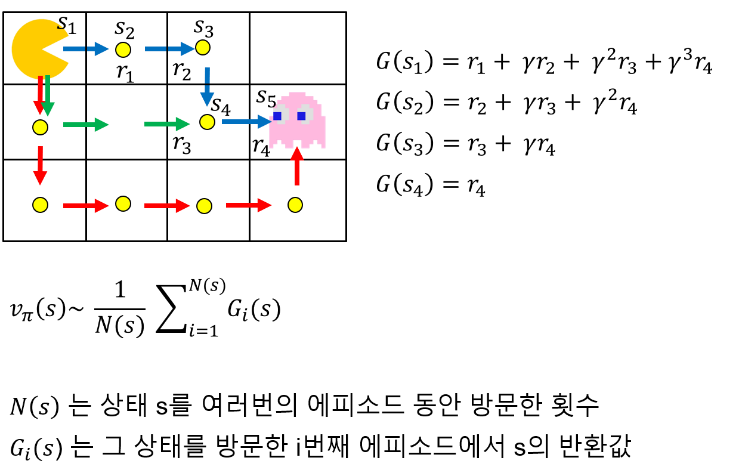
그림 4: Monte Carlo prediction -
몬테카를로 예측에서 에이전트는 아래의 업데이트 식을 통해 에피소드 동안 경험한 모든 상태에 대해 가치함수를 업데이트 함
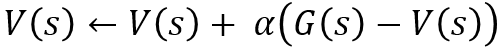
- 몬테카를로 예측에서 에이전트는 이 업데이트 식을 통해 에피소드 동안 경험한 모든 상태에 대해 가치함수를 업데이트 함
- 샘플 수 가 많아질수록 더 정확한 가치함수 최적화가 이루어짐
[4/6] 시간차 예측 (Temporal Difference Prediction)
-
몬테카를로 예측의 가장 큰 단점은 실시간이 아님. 다시말해, 한 에이전트의 한 에피소드가 끝나기 전까지는 가치함수의 업데이트를 할 수 없음
- 만약 에피소드가 정말 길어진다거나 끝이 없다면 몬테카를로 예측은 사용할 수 없음
-
아래 식에서 반환값은 그 에피소드가 끝나야 알 수 있음
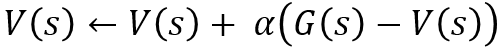
-
시간차 예측에서는 다음 스텝의 보상과 가치함수를 샘플링 하여 현재 상태의 가치함수를 업데이트 함
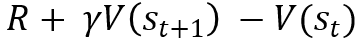
-
시간차 예측은 어떤 상태에서 행동을 하면 보상을 받고 다음 상태를 알게되고 다음 상태의 가치함수와 알게된 보상을 더해 그 값을 업데이트의 목표로 삼는다는 것. 이 과정을 반복함 (그림 5)
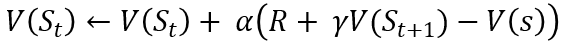

그림 5: Temporal difference prediction
-
시간차 예측은 매 타임스텝마다 현재 상태에서 하나의 행동을 하고 환경으로 부터 보상을 받고 다음 상태를 알게 됨
-
다음 상태의 예측값을 통해 현재의 가치함수를 업데이트 하는 방식을 강화학습에서는 부트스트랩(Bootstrap)이라고 함. 즉, 목표가 정확하지 않은 상태에서 현재의 가치함수를 업데이트 함
[5/6] 살사 (SARSA)
- 한줄요약: 살사 = 정책 이터레이션 + 가치 이터레이션
- 정책 이터레이션 = 정책 평가(예측) + 정책 발전(제어)
- 예측: 가치함수 학습
- 제어: 예측을 기반으로 정책을 발전 시킴
- 시간차 예측의 문제점은 가치함수를 현재상태에서만 업데이트함. 즉, 모든 상태에서의 정책을 발전시키기 어려움
- 이 문제를 살사에서는 가치 이터레이션을 통해 해결함
- 즉 살사 = 시간차 예측 + 탐욕정책(𝜀-greedy)
- 살사에서 업데이트 하는 대상은 가치함수가 아닌 큐함수임. 왜냐하면 현재상태의 정책을 발전시키려면 R_(t+1)+ γv_n (s’)의 최댓값을 알아야하는데 그러려면 정책에 대한 정보 (환경에 대한 정보)를 알야아하기 때문임
- 큐함수를 업데이트 하려면 샘플이 필요함. 살사에서는 [S_t, A_t,R_(t+1),S_(t+1),A_(t+1)]를 샘플로 사용함
- 앞에서 사용한 탐욕정책을 개선한 ε-탐욕정책을 사용함
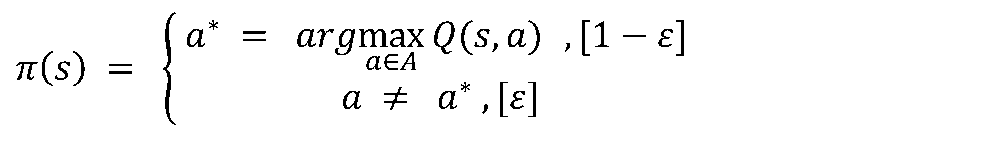
- 살사의 한계 (a.k.a On-Policy)
- 온폴리시(On-Policy)란 행동 정책과 학습 정책이 같은걸 의미
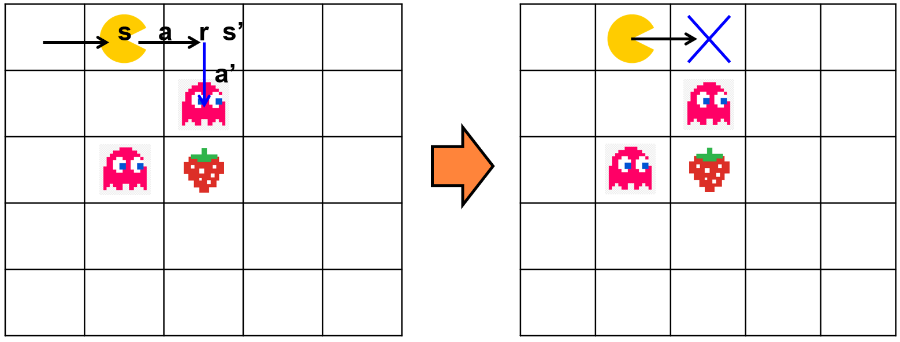
그림 6: The main disadvantage of the SARSA algorithm
[6/6] 큐러닝 (Q-Learning)
- 온폴리시 학습의 경우 탐험에서 문제점이 발생함
- 온폴리시에서 문제가 발생하는 이유가 행동 정책과 학습 정책이 같아서니까 그 둘이 다르면 되지 않을까???
- 큐러닝은 에이전트가 다음상태를 알게되면 그 상태에서 가장 큰 큐함수를 현재 큐함수의 업데이트에 사용함
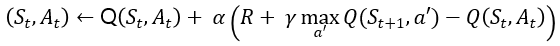
- 이와 같은 방식을 오프폴리시(Off-Policy)라고 함
- 큐러닝은 살사의 딜레마를 해결하기 위해 행동 선택은 𝜀-탐욕정책으로, 업데이트는 벨만 최적 방정싱으로 진행함